计算多边形的面积
计算一个多边形的面积有很多种方法。
对于一个多边形来说,凸多边形是特例中的特例,我们就以凸多边形为例来讨论这个问题。
方法一:三角形分割
通过分治思想,把凸多边形分割为若干个三角形,这样就容易计算面积了。
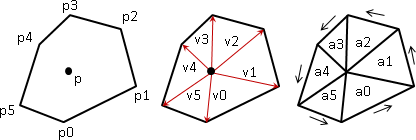
我们可以取多边形内的一个点,然后将改点依次与各边连线,这样多边形就被分割为多个三角形了。我们就可以使用外积来计算每个三角形的面积,然后加起来得到多边形的面积。
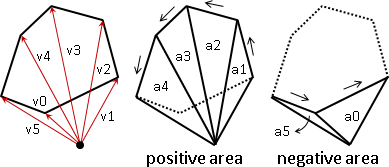
实际上,由于外积存在正负之分,这样我们选取的点不单单可以在凸多边形的内部,也可以在外部甚至是边界上。正值覆盖到多边形的面积,而负值刚好是多余图形的面积,正负相消,得到的就是多余图形的面积。
如果不限定基点的选取,那么选取原点最为方便,这样就不必刻意计算每个点的向量,可以直接拿相邻两点的坐标计算外积。
我们可以写成数学公式:
这里说明一下,如果按逆时针旋转,求出来的为正值;如果按顺时针旋转,求出来的为负值,还要再取绝对值。
方法二:积分方法
对于每一条边,我们可以将其对 x 轴进行积分,计算边与 x 轴与竖直边界围成的梯形的面积。
面积为
Point s,t; double area = (s.x+t.x)/2.0 * (s.x-t.x);
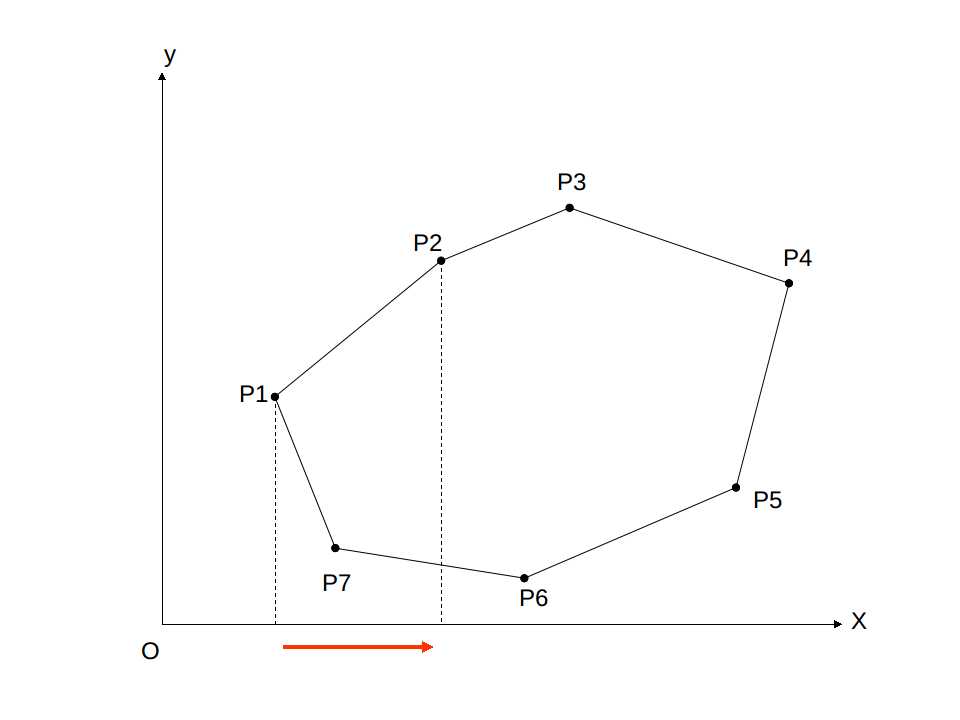
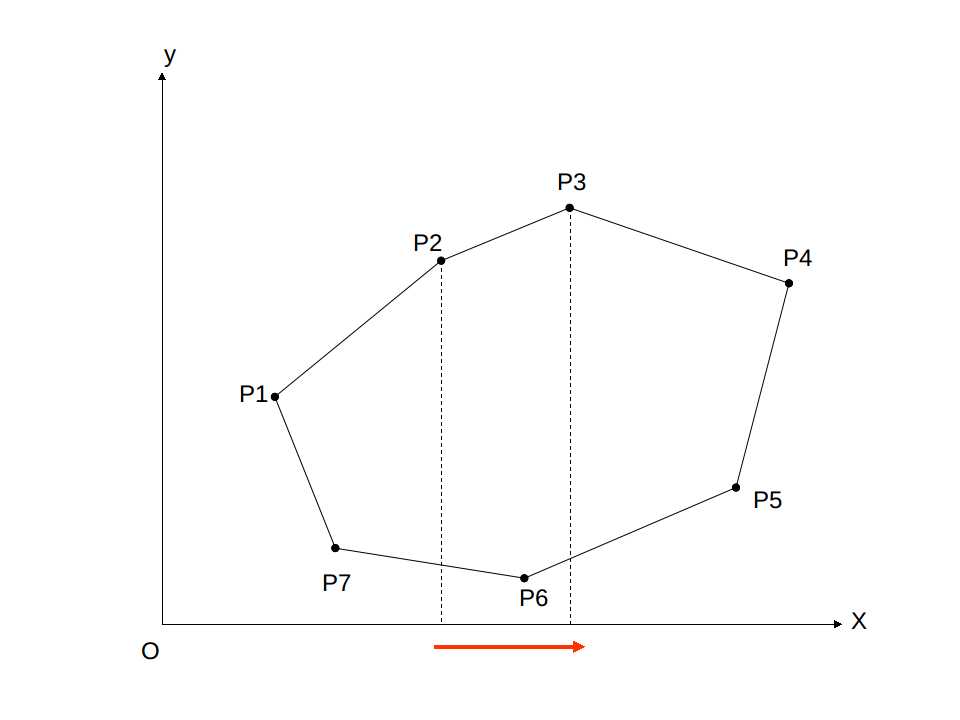
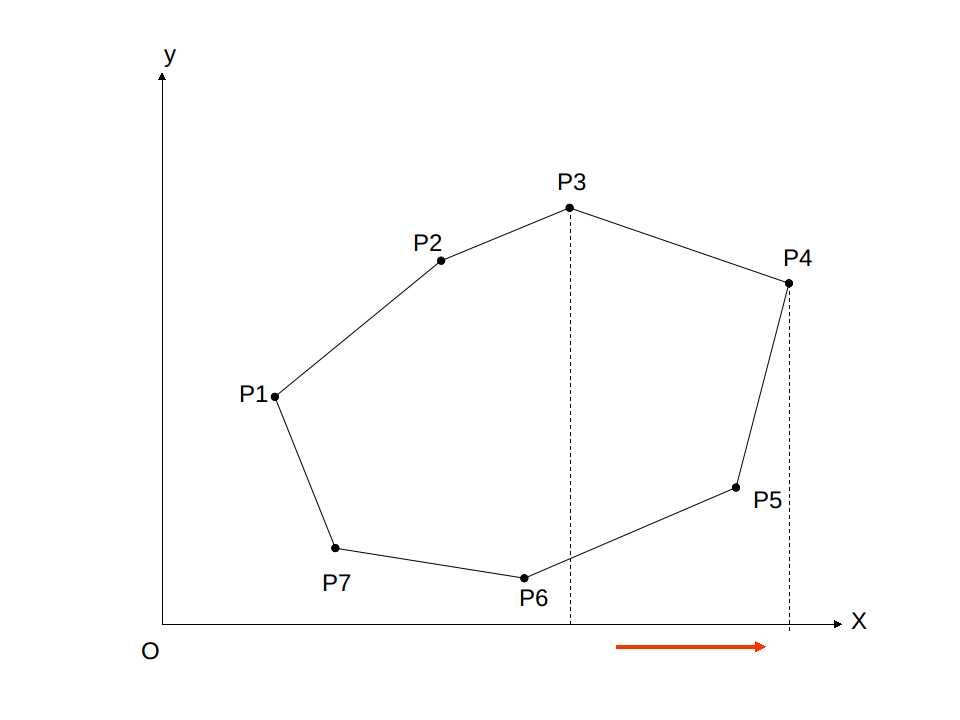
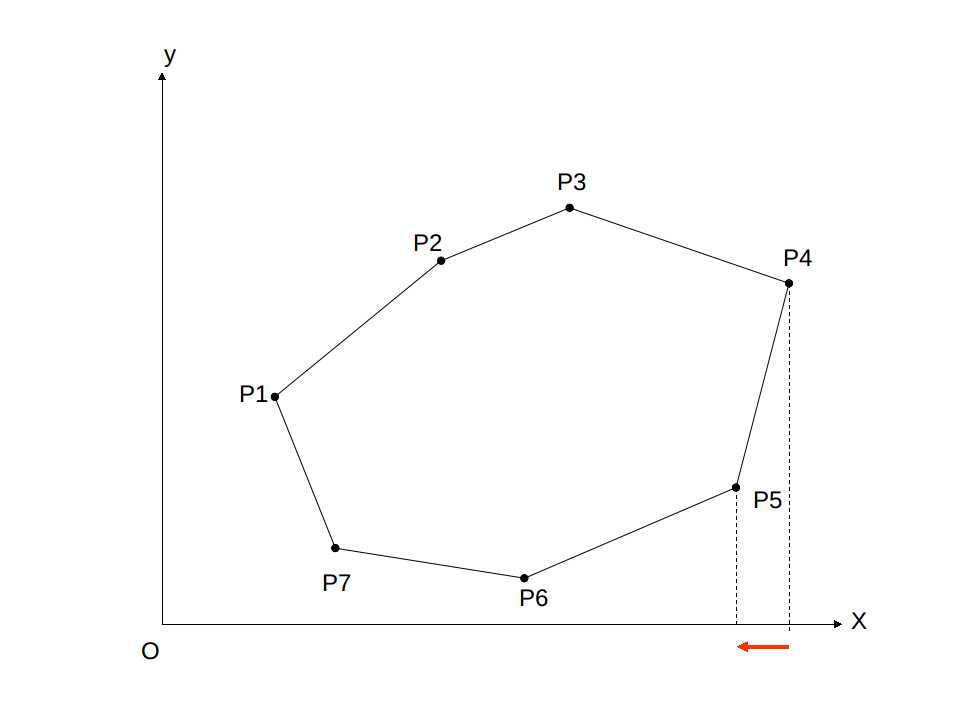
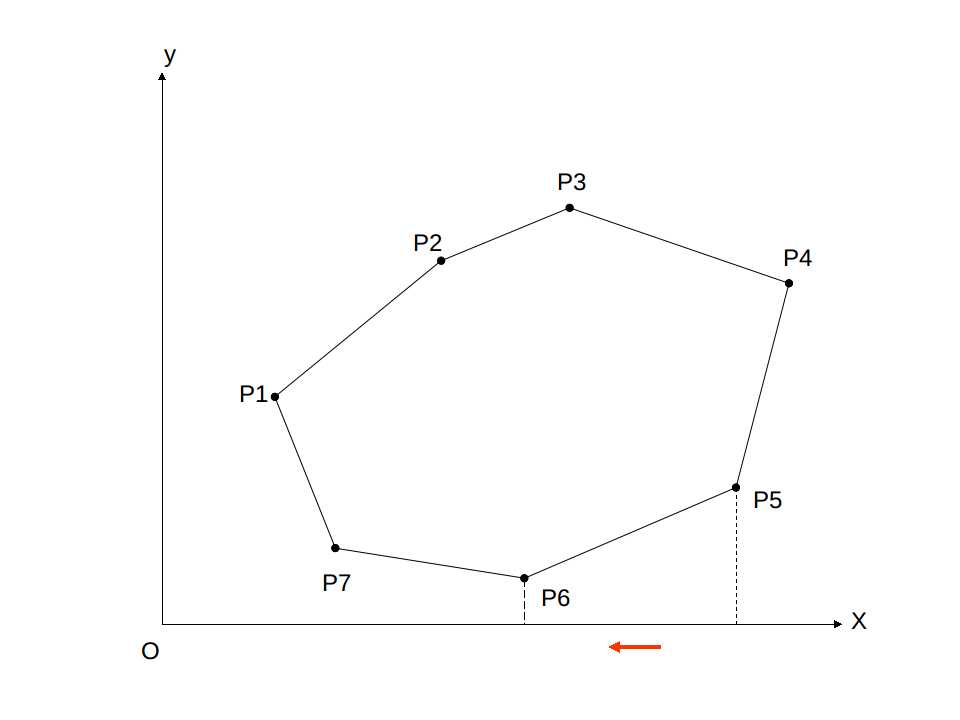
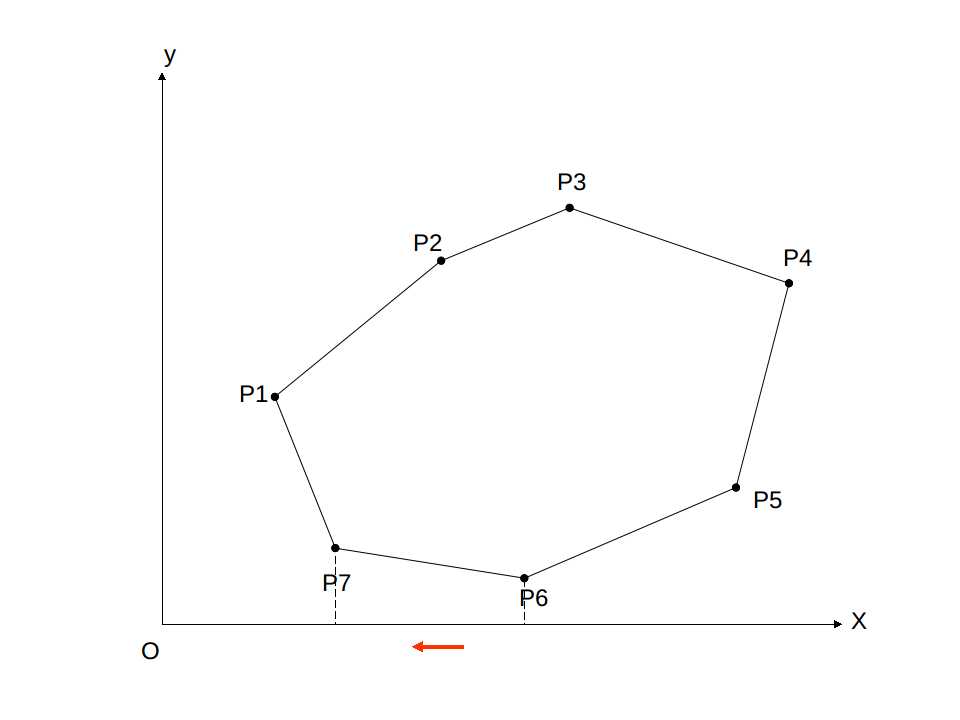
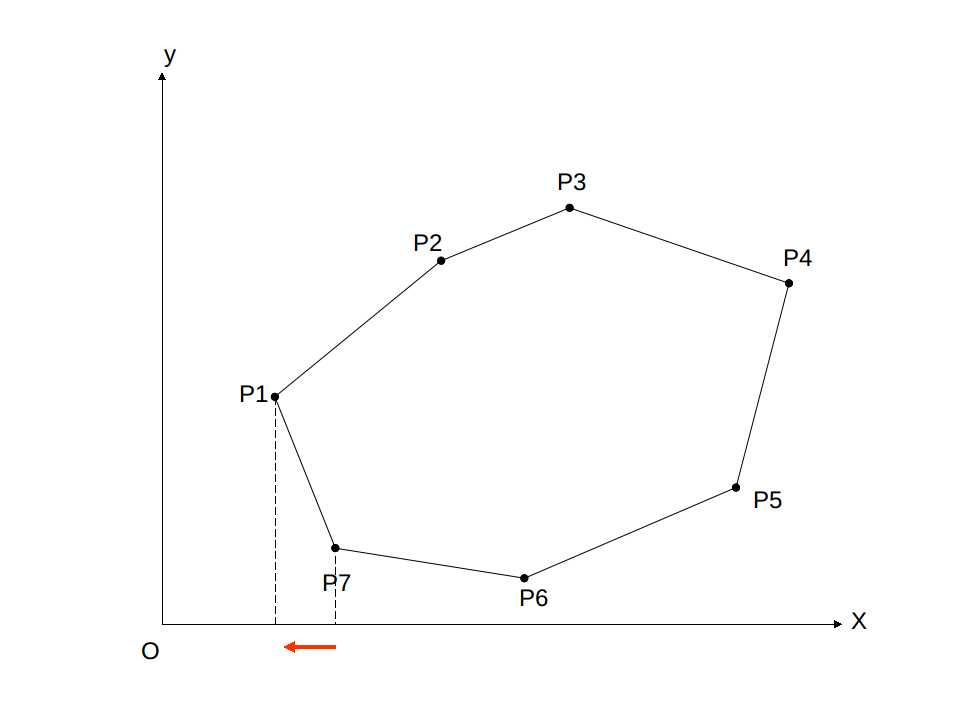
这里我们也要按照逆时针考虑,这样得到的面积也就存在正负之分,正好将多余部分抵消,得到面积。
应用
- 求解面积
这个就不用多说了,求解凸多边形的面积,这是必须的应用。
- 判断基点是否在凸多边形内
首先我们考虑一下【方法一】和【方法二】在计算面积上有什么不同。就是【方法一】需要选取基点,也就是说【方法二】计算得到的面积可以作为一个参考。这样,我们可不可以考虑通过这两个面积计算方法的不同点来判断基点的位置。
关键点就是【方法一】对于面积存在正负,如果我们不考虑面积的正负,而全部取绝对值,那么基点在凸多边形内和凸多边形外对于面积的计算就会存在一定的影响。
具体方法在 判断点是否在多边形内 一并讲解。