判断一个点是否在凸包(多边形)内
2013-08-01 算法 算法 计算几何 1.6k 字 4 分钟
判断一个点是否在凸包内是比较常用的一个算法。
判断一个点是否在凸包(多边形)内是比较常用的一个算法,总结了一下出现的方法,主要找到了下面的几种。
方法一:外积计算法(只适用于凸多边形)
简单来说就是将点到凸多边形的顶点的各条向量,通过外积运算判断是否都往同一方向旋转,如果都是往同一方向旋转,则表示点在凸多边形的内部;如果中途出现反方向旋转,则说明点在凸多边形的外部;如果中途出现为零的情况,表示点在凸多边形上,而且就在对应的边上。
时间复杂度为O(N)
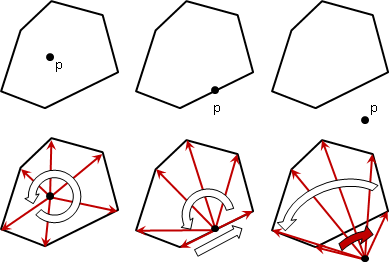
方法二:区域判别法
这种方法适用于快速判断多个点是否在一个凸多边形内。
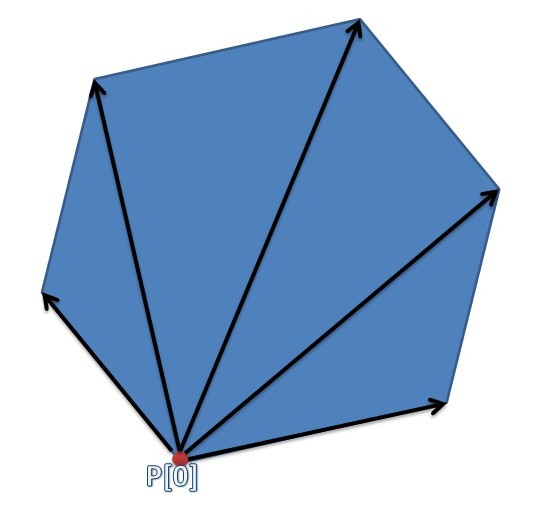
首先,将一个凸多边形划分为 N 个三角形的区域。
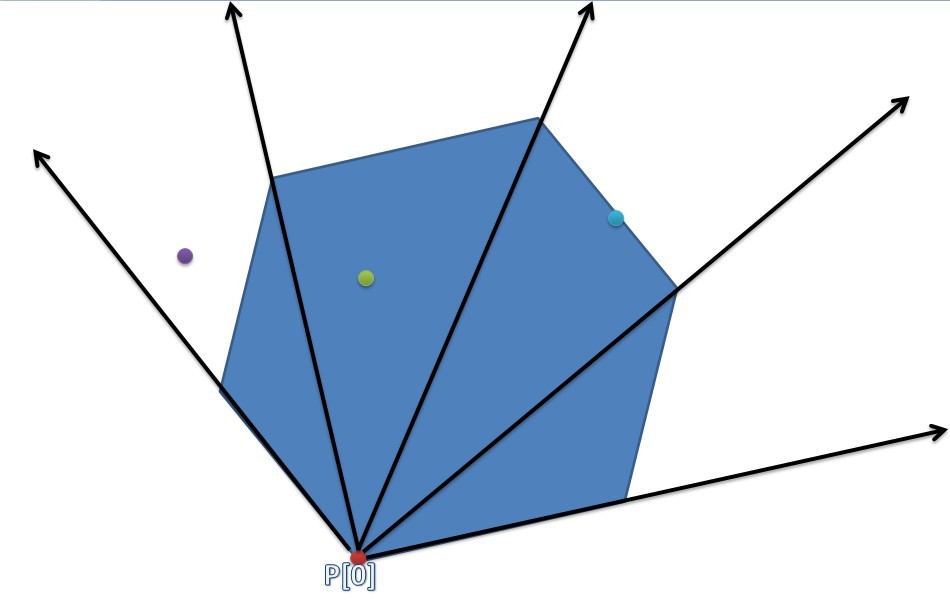
对于某一个点,如果不在这些三角形区域内,则必不在凸包内。否则就能通过二分的方法得到点所在的三角形区间。
最后只需判断点与原凸包边的关系即可。
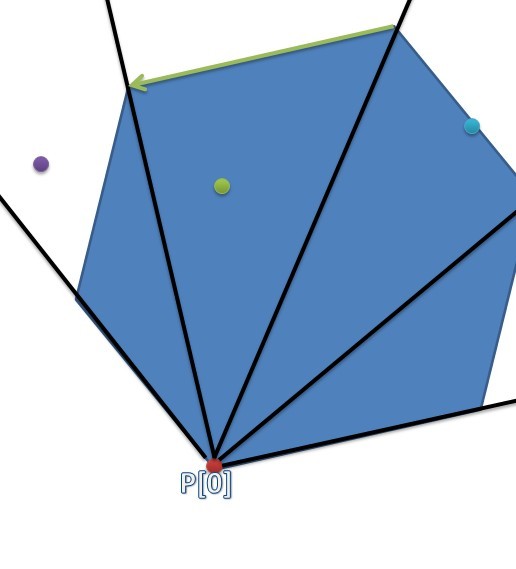
假设我们查询绿色的点是否在凸包内,我们首先二分得到了它所在的区间,然后判断它和绿色的向量的关系,蓝色和紫色的点类似,蓝色的点在边界上,紫色的点在边界右边。
由于应用了二分,时间复杂度为O(logN)。
问题链接:SGU253 Theodore Roosevelt
sgu253 这个问题需要使用极角序判断才能通过,而 cf116B 因为精度问题(把 eps 开到 1e-20 了都过不了)就需要使用叉乘判断,但是叉乘判断对于 sgu253 却不起作用。两题的方法不能通用,也不知道这是为什么?
sgu253 代码:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdio>
#define PI 3.14159265358979323846
#define PI_2 1.57079632679489661923
#define PI_4 0.78539816339744830962
#define eps 1e-6
#define DINF 1e200
using namespace std;
struct point
{
double x,y;
double ang;
point(){}
point(double _x,double _y){x=_x;y=_y;}
void read()
{
scanf("%lf%lf",&x,&y);
}
void write()
{
printf("%lf %lf\n",x,y);
}
};
bool dy(double x,double y) {return x > y + eps;} // x > y
bool xy(double x,double y) {return x < y - eps;} // x < y
bool dyd(double x,double y) {return x > y - eps;} // x >= y
bool xyd(double x,double y) {return x < y + eps;} // x <= y
bool dd(double x,double y) {return fabs( x - y ) < eps;} // x == y
double cross(point a,point b,point c)//向量 ac 在 ab 的方向
{
return (c.x - a.x)*(b.y - a.y) - (b.x - a.x)*(c.y - a.y);
}
double dis(point a,point b)
{
return(sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)));
}
int n,m,k;
point pt[100005];
point p[100005];
int cnt;
int pk;
int cmp(point a, point b)
{
return(xy(a.ang,b.ang) || (dd(a.ang,b.ang) && dis(a,pt[0])<dis(b,pt[0])));
}
int panduan(point x)
{
int l=1,r=n-1;
int mid;
int pos;
if(xy(x.ang,pt[l].ang) || dy(x.ang,pt[r].ang)) return 0;
while(l<r)
{
mid=(l+r)/2;
if(pt[mid].ang<=x.ang)
{
l=mid+1;
pos=l;
}
else
{
r=mid;
pos=r;
}
}
if(pos==n) pos--;
if(dyd(cross(pt[pos],pt[pos-1],x),0)) return 1;
return 0;
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
cnt=0;
pk=0;
for(int i=0;i<n;i++)
{
pt[i].read();
if(pt[pk].y>pt[i].y) pk=i;
else if(pt[pk].y==pt[i].y && pt[pk].x>pt[i].x) pk=i;
}
swap(pt[pk],pt[0]);
for(int i=0;i<n;i++)
{
pt[i].ang=atan2(pt[i].y-pt[0].y,pt[i].x-pt[0].x);
}
sort(pt+1,pt+n,cmp);
// for(int i=0;i<n;i++) pt[i].write();
pt[n]=pt[0];
for(int i=0;i<m;i++)
{
p[i].read();
p[i].ang=atan2(p[i].y-pt[0].y,p[i].x-pt[0].x);
}
for(int i=0;i<m;i++)
if(panduan(p[i]))
{
cnt++;
//cout<<i<<" ok"<<endl;
}
if(cnt>=k) puts("YES");
else puts("NO");
return 0;
}
CF116B 代码:(方法四提供了其它解法)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdio>
#define PI 3.14159265358979323846
#define PI_2 1.57079632679489661923
#define PI_4 0.78539816339744830962
#define eps 1e-10
#define DINF 1e200
using namespace std;
struct point
{
double x,y;
point(){}
point(double _x,double _y){x=_x;y=_y;}
void read()
{
scanf("%lf%lf",&x,&y);
}
void write()
{
printf("%lf %lf\n",x,y);
}
};
bool dy(double x,double y) {return x > y + eps;} // x > y
bool xy(double x,double y) {return x < y - eps;} // x < y
bool dyd(double x,double y) {return x > y - eps;} // x >= y
bool xyd(double x,double y) {return x < y + eps;} // x <= y
bool dd(double x,double y) {return fabs( x - y ) < eps;} // x == y
double cross(point a,point b,point c)//向量 ac 在 ab 的方向
{
return (c.x - a.x)*(b.y - a.y) - (b.x - a.x)*(c.y - a.y);
}
double dis(point a,point b)
{
return(sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)));
}
int n,m,k;
point pt[100005];
point p[100005];
int cnt;
int pk;
int cmp(point a, point b)
{
double ans = cross(pt[0], a, b);
if(ans < 0) return 1;
if(ans == 0 && (dis(a, pt[0]) <= dis(b, pt[0]))) return 1;
return 0;
}
int panduan(point x)
{
int l=0,r=n-1;
int mid;
int pos;
if(dd(cross(x,pt[0],pt[n-1]),0)) return 0;
if(dd(cross(x,pt[1],pt[0]),0)) return 0;
while(l<=r)
{
mid=(l+r)/2;
if(dyd(cross(x,pt[mid],pt[0]),0))
{
pos=mid;
l=mid+1;
}
else r=mid-1;
}
if(dyd(cross(x,pt[pos],pt[pos+1]),0)) return 0;
return 1;
}
int main()
{
scanf("%d",&n);
cnt=0;
pk=0;
for(int i=0;i<n;i++)
{
pt[i].read();
if(pt[pk].y>pt[i].y) pk=i;
else if(pt[pk].y==pt[i].y && pt[pk].x>pt[i].x) pk=i;
}
swap(pt[pk],pt[0]);
sort(pt+1,pt+n,cmp);
// for(int i=0;i<n;i++) pt[i].write();
pt[n]=pt[0];
scanf("%d",&m);
for(int i=0;i<m;i++)
{
p[i].read();
}
for(int i=0;i<m;i++)
if(!panduan(p[i]))
{
puts("NO");
return 0;
}
puts("YES");
return 0;
}
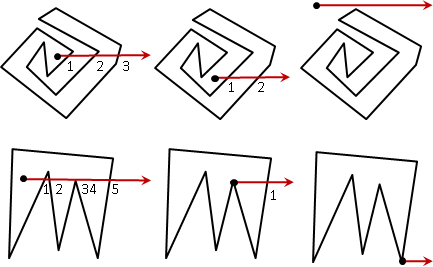
方法三:射线相交法
从给定的点开始,往随便一个方向(习惯水平向右)引一条无限长的射线,看看穿过多少条边。如果穿过偶数条边,说明点在多边形外;穿过奇数条边,说明点在多边形内。
需要注意的是射线可能穿过定点或与边重合的情况。还有点也可能在多边形的边界上。
时间复杂度为O(N)
struct Point {float x, y;} p[10];
// 无法正确判断点在多边形上的情况
bool point_in_polygon(Point& t)
{
bool c = false;
for (int i = 0, j = 10-1; i < 10; j = i++)
if ((p[i].y > t.y) != (p[j].y > t.y) &&
t.x < (p[j].x-p[i].x)*(t.y-p[i].y)/(p[j].y-p[i].y)+p[i].x)
c = !c;
return c;
}
补充两段代码:
代码一:
inline int dblcmp(double x) //判断double的符号
{
if(fabs(x) < eps)
return 0;
return x > 0 ? 1 : -1;
}
//判断点是否在多边形内
//思想:过点p做一条射线,判断交点数
bool point_inside(point p[],point& aa)
{
int i, cnt = 0;
double t;
//确保p[n] = p[0]
for(i=0;i<n;++i)
{
if((p[i].y<=aa.y && p[i+1].y>aa.y) ||
(p[i+1].y<=aa.y && p[i].y>aa.y))
{
if(!dblcmp(p[i].y-p[i+1].y))
{
if(dblcmp(p[i].y-aa.y)==0)
cnt++;
t=-DINF;
}
else
t=p[i+1].x-(p[i+1].x-p[i].x)*(p[i+1].y-aa.y)/(p[i+1].y-p[i].y);
if(dblcmp(t-aa.x)>=0)
cnt++;
}
}
return cnt%2;
}
代码二:
bool isIntersected(point s1,point e1,point s2,point e2) //判断线段 s1-e1 与线段 s2-e2 是否相交
{
return ( max(s1.x,e1.x)>=min(s2.x,e2.x) &&
max(s1.y,e1.y)>=min(s2.y,e2.y) &&
max(s2.x,e2.x)>=min(s1.x,e1.x) &&
max(s2.y,e2.y)>=min(s1.y,e1.y) &&
cross(s2,e1,s1)*cross(e1,e2,s1)>=0 &&
cross(s1,e2,s2)*cross(e2,e1,s2)>=0 );
}
bool online(point p1,point p2,point p) //判断点 p 是否在线段 p1-p2 上
{
if(fabs(cross(p1,p2,p))<eps && ((p.x-p1.x)*(p.x-p2.x)<eps && (p.y-p1.y)*(p.y-p2.y)<eps))
return true;
return false;
}
//判断点是否在多边形内
//思路:取一条无限长的线段,判断线段与线段相交
bool In_Polygon(point p[],point cen)
{
int cnt=0;
point PINF=point(20000.0,cen.y);
for(int i=0;i<n;i++){
if(online(p[i],p[i+1],cen)) return false;
if(fabs(p[i].y-p[i+1].y)<eps) continue;
if(online(cen,PINF,p[i])){
if(p[i].y>p[i+1].y) cnt++;
}
else if(online(cen,PINF,p[i+1])){
if(p[i+1].y>p[i].y) cnt++;
}
else if(isIntersected(cen,PINF,p[i],p[i+1]))
cnt++;
}
return cnt&1;
}
方法四:面积比较法
我们知道计算面积有两种方法(具体可以参考【计算多边形的面积】),而两种方法的区别是关于有没有使用基点。
于是对于存在基点的方法,如果基点在多边形内,那么划分三角形得到的面积的符号都是相同的(逆时针计算的话都为正)。但是如果基点选在多边形外,就会出现相反符号的面积抵消的情况。这样来说,如果我们都按绝对值来计算每个划分三角形的面积,那么基点在多边形外的到的面积将会比真正的面积大。
我们可以通过积分方法和基点方法分别计算面积,然后通过比较两种方法的面积判断基点的位置。如果面积相等,则说明基点在多边形内;如果不相等,则说明基点在多边形外。
struct node
{
double x, y;
}p[105];
int n; //定点的数目
double getareap(node st)//多边形面积
{
int i;
double sum = 0;
node p1, p2;
p1 = p[n-1];
for(i = 0; i < n; i ++)
{
p2 = p[i];
sum += (p1.y+p2.y) * (p1.x - p2.x);
p1 = p2;
}
return fabs(sum/2);
}
double areat(node p0, node p1, node p2)//三角形面积,面积取绝对值
{
return fabs((p1.x-p0.x)*(p2.y-p0.y) - (p2.x-p0.x)*(p1.y-p0.y));
}
double getareat(node st)
{
int i;
double sum = 0;
p[n] = p[0];
for(i = 0; i < n; i ++)
{
sum += areat(st, p[i], p[i+1]);
}
return sum/2.0;
}
int inpolygon(node st)//点在多边形内判断,st 为基点
{
double ans1, ans2;
ans1 = getareap(st);
ans2 = getareat(st);
if(fabs(ans1-ans2) < ep) return 1;
return 0;
}
方法五:共求凸包法
在codeforces的一道题目里看到的这种方法,适用于点比较多的情况。
大体思路是将凸包上的点与内部的点共同求凸包,如果最后求得的凸包中出现了原先没有出现的点,则证明有些点不严格在凸包内部。
题目链结:Codeforces 166B Polygons
这里大体讲解一下代码。题目要求的是严格在凸包内,那么就要求即使存在共线的点,也要出现在凸包上。
这里提供两组cf上的测试数据
Test: #16
4
-10 -10
-10 10
10 10
10 -10
3
-10 0
1 5
2 2
Test: #42
4
-10 -10
-10 10
10 10
10 -10
3
10 0
2 2
1 5
可以看出,这两组测试数据形式上差不多,关键在于共线点存在的位置。这里为了使共线点出现在最后的凸包上,我们把最左上角的点和最右下角的点的连线作为参考线。在参考线右边的可以考虑按距离近的先排序,在参考线左边的可以考虑按距离远的先排序,这样的目的是为了保证真正的极角排序是按照逆时针(或顺时针) 形成的。这就有了下面代码的 cmp 函数。
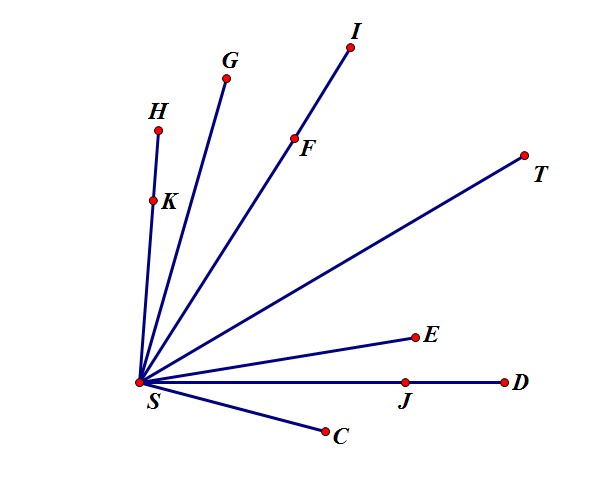
图片中点极角序是 S->C->J->D->E->T->I->F->G->H->K
如果先K再H,k点一定会被弹出,但是先H再K就不会。
我的渣代码:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
using namespace std;
struct point
{
long long x,y;
int flag;
}tmp,pld,pru;
vector<point>VI;
vector<point>Q;
int n,m;
long long cross(point a,point b,point c) //求叉积
{
return((a.x-c.x)*(b.y-c.y)-(a.y-c.y)*(b.x-c.x));
}
long long dis(point a,point b)
{
return((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
//int cmp(point a, point b)
//{
// double ans = cross(a, b, tmp);
// if(ans > 0) return 1;
// if(ans == 0 && (dis(a, tmp) <= dis(b, tmp))) return 1;
// return 0;
//}
int cmp(point a,point b) //当两点共线的时候,则根据与标准线的位置决定距离问题
{
if(cross(a,b,pld)!=0)
{
return cross(a,b,pld)>0;
}
else
{
if(cross(pld,a,pru)>=0)
return dis(a,pld)<dis(b,pld);
else
return dis(a,pld)>dis(b,pld);
}
}
int ld; //记录最左下角点的位置
int ru; //记录最右上角点的位置
int main()
{
VI.clear();
ld=ru=0;
//将凸包点加入点集合中
cin>>n;
for(int i=0;i<n;i++)
{
cin>>tmp.x>>tmp.y;
tmp.flag=1;
VI.push_back(tmp);
if(VI[ld].x<VI[VI.size()-1].x) ld=VI.size()-1;
else if(VI[ld].x==VI[VI.size()-1].x && VI[ld].y<VI[VI.size()-1].y) ld=VI.size()-1;
if(VI[ru].x>VI[VI.size()-1].x) ru=VI.size()-1;
else if(VI[ru].x==VI[VI.size()-1].x && VI[ru].y>VI[VI.size()-1].y) ru=VI.size()-1;
}
//将内部点加入点集合中
cin>>m;
for(int i=0;i<m;i++)
{
cin>>tmp.x>>tmp.y;
tmp.flag=2;
VI.push_back(tmp);
if(VI[ld].x<VI[VI.size()-1].x) ld=VI.size()-1;
else if(VI[ld].x==VI[VI.size()-1].x && VI[ld].y<VI[VI.size()-1].y) ld=VI.size()-1;
if(VI[ru].x>VI[VI.size()-1].x) ru=VI.size()-1;
else if(VI[ru].x==VI[VI.size()-1].x && VI[ru].y>VI[VI.size()-1].y) ru=VI.size()-1;
}
pld=VI[ld];
pru=VI[ru];
swap(VI[ld],VI[0]);
sort(VI.begin()+1,VI.end(),cmp);
VI.push_back(pld);
Q.clear();
Q.push_back(VI[0]);
Q.push_back(VI[1]);
for(int i=2;i<VI.size();i++)
{
while(cross(Q[Q.size()-2],VI[i],Q[Q.size()-1])>0) Q.pop_back();
Q.push_back(VI[i]);
}
//cout<<Q.size()<<endl;
int flag=1;
for(int i=0;i<Q.size();i++)
{
if(Q[i].flag==2)
{
flag=0;
break;
}
}
if(flag) puts("YES");
else puts("NO");
return 0;
}
我还发现还有其它的一些代码是相同的思路,但是使用了不同的实现方法。将点按坐标排序之后,然后求一个正向凸包,再求一次逆向凸包。最后就出结果了???还在考虑这是为什么。
后来还是看了看,似乎明白了点。
上面也提到了,前部分和后部分对于相同极角序的距离判断是不同的。极角序小的时候距离小的在前边,而极角序大的时候,正好想法。
现在我们不考虑极角序对于距离的影响,统一进行相同的排序,那么在求凸包的时候正向凸包会把一些极角共线点包含进去,然后当反向求凸包的时候又会吧另一些极角共线点包含进去。由于正序和逆序对于严格的凸包上的点没有什么影响,不同的只是一些共线点的多少,通过两次求解凸包就会把所有的极角共线点包含进去,从而解决了分开排序的问题。
//by mystery_boy
/*
TASK: Polygons
LANG: C++
*/
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<algorithm>
#include<map>
#include<set>
#include<list>
#include<queue>
#include<iostream>
using namespace std;
#define X first
#define Y second
int N,M,T;
typedef long long CoordType;
struct Point {
CoordType x, y, z;
bool operator <(const Point &p) const {
return x < p.x || (x == p.x && y < p.y);
}
}temp;
// 2D cross product.
// Return a positive value, if OAB makes a counter-clockwise turn,
// negative for clockwise turn, and zero if the points are collinear.
CoordType cross(const Point &O, const Point &A, const Point &B)
{
return (A.x - O.x) * (B.y - O.y) - (A.y - O.y) * (B.x - O.x);
}
// Returns a list of points on the convex hull in counter-clockwise order.
// Note: the last point in the returned list is the same as the first one.
vector<Point> convexHull(vector<Point> P)
{
int n = P.size(), k = 0;
vector<Point> H(2*n);
// Sort points lexicographically
sort(P.begin(), P.end());
// Build lower hull
for (int i = 0; i < n; i++) {
while (k >= 2 && cross(H[k-2], H[k-1], P[i]) < 0) k--;
H[k++] = P[i];
}
// Build upper hull
for (int i = n-2, t = k+1; i >= 0; i--) {
while (k >= t && cross(H[k-2], H[k-1], P[i]) < 0) k--;
H[k++] = P[i];
}
H.resize(k);
return H;
}
vector<Point> v,ans;
int main()
{
//freopen("xxx.in","r",stdin);
//freopen("xxx.out","w",stdout);
int i,j,k;
scanf("%d",&N);
for(i=1;i<=N;i++)
{
scanf("%I64d%I64d",&temp.x,&temp.y);
temp.z=1;
v.push_back(temp);
}
scanf("%d",&M);
for(i=1;i<=M;i++)
{
scanf("%I64d%I64d",&temp.x,&temp.y);
temp.z=2;
v.push_back(temp);
}
ans=convexHull(v);
bool ok=true;
for(i=0;i<ans.size();i++)
{
if(ans[i].z==2) ok=false;
// printf("%I64d %I64d [%I64d]\n",ans[i].x,ans[i].y,ans[i].z);
}
if(ok) printf("YES\n");
else printf("NO\n");
scanf(" ");
}
参考内容





