LeetCode Q137 Single Number II的数电AC方法
2017-04-27 算法 面试 算法 数字电路 556 字 1 分钟
最近突然在LeetCode上刷起了题目,Q137题和好久之前做过的数组中只出现过一次的元素类似。一个数组中有一些整数,这些数要不出现3次,要不只出现1次,并且出现1次的数字只有一个,找出那个出现一次的数字。
朴素的解法
根据之前的思路,可以弄一个大小32的数组,将数字对应的二进制位累计到对应的数组中,对数组模3后,剩下的数字就是只出现一次的数字。
public int singleNumber(int[] nums) {
int[] bts = new int[32];
for (int num : nums) {
for (int i = 0; i < bts.length; i++) {
bts[i] += ((num >> i) & 1);
}
}
int ans = 0;
for (int i = 0; i < bts.length; i++) {
ans |= (bts[i] % 3 << i);
}
return ans;
}
这个思路很好理解,也顺利解决了问题,但是在看其他人的解法时发现了一种奇特的解法:
public int singleNumber(int[] A) {
int ones = 0, twos = 0;
for(int i = 0; i < A.length; i++){
ones = (ones ^ A[i]) & ~twos;
twos = (twos ^ A[i]) & ~ones;
}
return ones;
}
完全无法理解😱。。。经过舍友的指点,原来灵感来自 数字电路 的范畴。本科期间也学过一些数字电路的知识,现在大部分已经还给老师了,根据记忆稍微弄一弄吧。
模型抽象——三进制加法
分析问题,原问题可以抽象成一个三进制的加法。有三个状态,保证累加到3个数字后可以抵消掉变为0,于是可以得到如下的状态转移图:
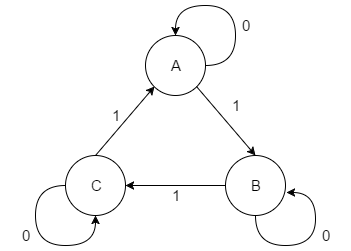
这个状态的图的状态不需要化简,现在为其分配状态值。共有三个状态,需要2位表示。
A -- 00
B -- 01
C -- 10
根据状态转移图,画出状态转移表。

按位拆分状态转移表,通过卡诺图,化简表达式。
这个卡诺图是按照高位画出的:

同理,低位的同样画出:

将相邻的“1”用红圈圈出,写出表达式:F1表示高位, F2表示低位。
F1=XZ+YZ
F2=YZ+XYZ
不容易,一步一百度,终于搞出了这个式子了。
程序编写
根据上面得到的两个表达式,可以写出以下的程序:
高位用变量a表示表达式中的X,低位用变量b表示表达式中的Y,输入Z就是数组中的数字了。
public int singleNumber(int[] nums) {
int a = 0;
int b = 0;
for (int num : nums) {
int ta = (a & ~num) | (b & num);
int tb = (b & ~num) | (~a & ~b & num);
a = ta;
b = tb;
}
return b;
}
提交测试一下,AC了。。。又解决了一个题目,可喜可贺😛。。。
